Prijsvragen

1. Wat is de naam van deze boog?
2. Zoek op internet een verklaring die volgens jou betrouwbaar is en stuur de link naar ons door.
3. Wat is een maanboog?

1. Dat is een mistboog
2. https://www.weerplaza.nl/weerinhetnieuws/weerweetjes/wat-is-een-mistboog-of-wolkenboog/5090/. Deze bron lijkt mij zeer betrouwbaar aangezien de auteur Raymond Klaassen al 30 jaar meteoroloog is. https://twitter.com/raymondklaassen?lang=en.
3. Regenbogen worden doorgaans geassocieerd met zonlicht, maar ook krachtig maanlicht, zoals bij volle maan, kan een regenboog veroorzaken. Deze boog is echter veel zwakker van kleur of zelfs kleurloos, doordat we 's nachts slecht kleuren zien. Een maanboog ziet er daardoor meestal witachtig uit.
   https://wibnet.nl/natuur/weer/regenbogen-zijn-er-in-soorten-en-maten


Verder besloten we een bonus uit te keren aan Dina Talhaoui uit vwo 5 van het Theresialyceum in Tilburg. Zij voegde aan haar antwoord een fraaie poster toe en verwerkte daar bovendien een foto van een maanboog in. Zie Poster Dina Talhaoui.pdf.


Prijsvraag 47: Een ruimtewiel

In een sciencefiction verhaal beweegt een enorm wielvormig ruimtestation (d = 100 km) op een hoogte h boven de evenaar.

Vanaf de aarde gezien lijkt het ruimtestation net zo groot als de volle maan.
 –  Is de baan geostationair? Licht je antwoord met een berekening toe.

Er kwamen twee goede antwoorden binnen, van:
Zayar Lin, uit 5H van het Beekdal Lyceum in Arnhem en
Jip Oude Weernink, uit 5^e van het Praedinius Gymnasium in Groningen.

Omdat er de laatste tijden weinig reacties kwamen op onze prijsvragen, hebben we dit keer niet geloot. Beiden krijgen dus een prijs van € 25.

Oplossing
Onze oplossing ziet er zo uit:

Als het wiel en de maan even groot lijken, dan zie je ze onder dezelfde hoek.



Met verhoudingen in de twee rechthoekige driehoeken kun je dan h uitrekenen: h = 11·10³ km.
Het antwoord op de vraag is: nee, want een satelliet in een geostationaire baan zit hoger, namelijk op 36·10³ km.

Iets andere manier:
De diameter van de maan is ongeveer 35 keer groter dan het ruimtewiel, dus h is dan 35 keer zo klein. Dan kom je ook uit op 11·10³ km.

De gebruikte getallen kun je op internet opzoeken.



Prijsvraag 46: μ

In deze film zie je hoe een blokje aan een losse katrol (m_totaal = 47,8 g) een blokje op tafel voortsleept (M = 123,3 g).



Met een videometing zijn de h(t)-grafiek en de x(t)-grafiek gemaakt.
• Bepaal de wrijvingscoëfficiënt μ.


De h(t)-grafiek van het blokje aan de katrol




De x(t)-grafiek van het voortgesleepte blokje


Voor deze prijsvraag kwamen geen goede oplossingen binnen.

Oplossing
De arbeid van de zwaartekracht op m wordt omgezet in wrijvingsarbeid op M:
m·g·Δh − F_w·Δx = 0  met  F_w = μ·M·g
Δh = 0,13 m  en  Δx = 0,25 m
0,13·47,8 = 0,25·μ·123,3  dus  μ = 0,20



Prijsvraag 45: Een tunnel door de aarde

Een steen die door een tunnel in de aarde valt, zal aan de overzijde terugveren. Deze trilling duurt net zo lang als een aardscheerder doet over zijn rondje.



Tot onze verrassing kwam er voor deze niet al te moeilijke prijsvraag geen enkele inzending.



Prijsvraag 44: Rondslingeren

Twee identieke ballen zijn star verbonden met identieke spaken. De ballen worden vanuit middelpunt M rondgeslingerd in een horizontaal vlak. De massa's van de spaken zijn te verwaarlozen.
Als in spaak L₂ een spankracht van 10 N werkt, hoe groot is dan de spankracht in L₁?







Prijsvraag 43: Een stoombootje

Bekijk het filmpje van dit stoombootje.



Water dat door het vlammetje in de ketel tot stoom wordt gemaakt, wordt door twee buisjes uitgestoten. Het spoor toont een interferentiepatroon dat ontstaat doordat die uitlaten in fase uitstoten. Er wordt per seconde evenveel water aangezogen als weggeblazen. Toch beweegt het bootje vooruit. Hoe kan dat?

Oplossing
De ketel vul je via een van de buisjes, het teveel loopt weg door het andere buisje. Al na een paar seconden zorgt de vlam voor stoom in de ketel, die ontsnapt door de buisjes. De stoom neemt daarbij water mee en het bootje ondervindt een naar voren gerichte impuls. Vergelijk met een kaars die je wel kunt uitblazen maar niet kunt 'uitzuigen'.
Er was één goede inzending. Daniel Salomonson uit 5 havo van het Geert Grote College in Amsterdam zond ons deze schets:






Prijsvraag 42: Zonder wiel

De verkeerswet laat dit niet toe, maar welke natuurkundewet wel?



Oplossing
Er waren verschillende goede inzendingen zodat we moesten loten.
De prijs gaat naar Vicky van der Burgt uit 6Vc van het Elzendaalcollege in Boxmeer.
De momentenwet / hefboomwet is de natuurkundewet die hier aan de orde is.



Prijsvraag 41: π in het Oude Testament

π is oud! Hij staat al in 1 Koningen 7:23 en 2 Kronieken 4:2. Daar lezen we over het metaalwerk van Salomo's tempel:
"Voorts maakte hij de zee, van gietwerk, tien el van rand tot rand, geheel rond, vijf el hoog, terwijl een meetsnoer van dertig el haar rondom kon omspannen."

Er waren verrassend weinig inzendingen voor deze niet al te moeilijke prijsvraag. Corona-sores?
De prijs ging naar Lieke Buiter uit 5H3 van het Assink lyceum, locatie Bouwmeester.
Zij schreef ons:
omtrek = π * diameter
diameter = 10 el en omtrek = 30 el
30 = π * 10 ==> π = 30/10 = 3,0
Volgens het Oude Testament is π gelijk aan 3.



Prijsvraag 40: Een zwevend blikje

Het blikje met pennen op de linker foto lijkt te zweven. De middelste foto verklaart de truc. Een van ons verdreef zijn lockdown-verveling met het maken van de opstelling van de rechter foto.



Als je op het internet zoekt onder de naam tensegrity vind je heel veel voorbeelden met mooie plaatjes en duidelijke filmpjes die uitleggen wat er aan de hand is.
Maak zelf een tensegrity opstelling (met Lego, satéprikkers, hout, ijzer, ...) en stuur een foto van jouw geknutsel op naar stevin@stevin.info; verdien hiermee € 25.

Ruthger Eygendaal, uit VWO 6A van de SG Spieringshoek in Schiedam stuurde deze foto op:





Prijsvraag 39: Een trillend spoeltje



Bekijk het filmpje. De batterij staat op een stapel magneten. De onderkant van het spoeltje zit vast.
Beredeneer waar de noordpool van de stapel magneten zich bevindt.

Oplossing
Marthe de Vries uit 5^E van het Praedinius Gymnasium in Groningen stuurde een goede oplossing in.

We zien in het filmpje dat het spoeltje wordt afgestoten door de magneetjes. Als we van bovenaf op de spoel kijken weten we dat de stroom door de windingen tegen de klok in gaat. Als we de rechterhand regel gebruiken weten we dat de noordpool van de spoel dus aan de plus-kant van de batterij moet zitten. De zuidpool van de spoel zit dus aan de min-kant. De zuidpool van de magneetjes moet dus ook aan de bovenkant zitten, omdat zuid en zuid elkaar afstoten; wat betekent dat de noordpool van de stapel magneetjes aan de onderkant zit.



Prijsvraag 38: Dollar Bill Vanish

Op de site Dollar Bill Vanish is een illusie te vinden die in strijd lijkt met de wetten van de natuurkunde.
• Klik op Download Activity
• Klik op Watch the Video
• Klik op Behind the Magic


Maak je eigen ontwerp - of verzin nog iets veel leukers! - en stuur voor 29 maart 12:00 uur (een link van) je video op naar stevin@stevin.info.

Er werd helaas geen video van een eigen ontwerp ingestuurd.



Prijsvraag 37: Drie lucifers

Een lucifer ligt los op tafel. Met nog twee andere lucifers lukt het om er een zware katrol aan te hangen.
• Bekijk de film Drie lucifers en verklaar het evenwicht.




Oplossing
Er waren slechts een paar inzendingen, maar die van Vicky van der Burgt uit 5Vc van het Elzendaalcollege in Boxmeer sprong er echt uit. Naar haar gaat de prijs.



Uit het plaatje dat zij bijvoegde is goed te zien dat de zware katrol nu onder de tafel aan het blauwe touwtje hangt en niet ernaast. Bij het groene punt bevindt zich de horizontale lucifer. Die wordt door de derde lucifer (rood) onder de tafel gedrukt.






Prijsvraag 36: Homoniem

Woorden zijn elkaars homoniem als ze hetzelfde geschreven worden, maar verschillende betekenissen hebben. Bijvoorbeeld: slot kan betekenen kasteel of sluiting of het eind van een verhaal.
In de achtbaan heeft Lenno een homoniem bedacht.

• Welk?


Oplossing
Er waren verschillende goede inzendingen met het homoniem kurkentrekker. De prijs gaat naar Martijn Verberk uit vwo 5 van het Walburg College in Zwijndrecht. Hij gaf er de uitleg bij dat Lenno de truc gebruikt van de FBI-regel/kurkentrekkerregel van p. 194 uit Stevin vwo.






Prijsvraag 35: Black Box

Vijf identieke lampjes (1 t/m 5) zijn aangesloten op dezelfde spanningsbron. Lampje 3 en 5 branden even fel en lampje 1 brandt minder fel. Lampje 2 en 4 geven wel licht, maar dat is bijna niet te zien.



We draaien enkele lampjes los en kijken wat er dan gebeurt:




Losgedraaid		Waarneming
Lampje 1		2 t/m 5 branden even fel
Lampje 2		1, 3 en 5 branden even fel 4 brandt niet
Lampje 3		Alles uit
Lampje 4		1, 3 en 5 branden even fel 2 brandt niet
Lampje 5		Alles uit
Lampje 1 + 2		Alles uit
Lampje 1 + 4		Alles uit
Lampje 2 + 4		1, 3 en 5 branden even fel



Oplossing
Er zijn verschillende goede schakelingen ingeleverd, maar we hebben dit keer niet geloot. De oplossing van Ben Weijers uit 5Va van het Elzendaalcollege in Boxmeer sprong er uit door de mooie figuur en doordat hij als enige inging op de lichtsterkte van de lampjes. De prijs gaat dus naar hem.

Hierboven zie je hoe de schakeling er uitziet, hieronder volgt de uitleg.
Losgedraaid:
Lampje 1: Alle lampen op 1 na kunnen branden omdat er een gesloten kringloop is. Route: 3, 5, 2, 4.
Lampje 2: Lampjes 3, 5 en 1 kunnen branden omdat er een gesloten kringloop is. Route: 3, 5, 1. Lampje 4 is uit omdat dit in serie staat met Lampje 2 en dus geen gesloten kringloop heeft.
Lampje 3: Alle lampjes staan uit, aangezien hoe je ook van plus naar min toe gaat, je komt altijd bij lampje 3, dus als dit los is, is er geen gesloten kringloop en staat alles uit.
Lampje 4: Lampjes 3, 5 en 1 kunnen branden omdat er een gesloten kringloop is. Route: 3, 5, 1. Lampje 2 is uit omdat dit in serie staat met lampje 4 en dus geen gesloten kringloop heeft.
Lampje 5: Alle lampjes staan uit, aangezien hoe je ook van plus naar min toe gaat, je komt altijd bij lampje 5, dus als dit los is, is er geen gesloten kringloop en staat alles uit.
Lampje 1 en 2: Als lampje 1 en 2 uit staan kun je op geen enkele manier van plus naar min gaan zonder lampje 1 of 2 tegen te komen, daardoor is er geen gesloten kringloop.
Lampje 1 en 4: Als lampje 1 en 4 uit staan kun je op geen enkele manier van plus naar min gaan zonder lampje 1 of 4 tegen te komen, daardoor is er geen gesloten kringloop.
Lampje 2 en 4: Alle lampen doen het gewoon behalve de losgedraaide lampen. Er is namelijk een mogelijkheid om van plus naar min te gaan, zonder een losgedraaid lampje tegen te komen.
Route: 3, 5, 1.

Felheid van de lampen
De felheid van de lampen heeft te maken met het feit dat de spanning die de energiebron levert niet hoog genoeg is. Laten we veronderstellen dat de spanning die de energiebron levert 10V is en dat elk lampje 4V nodig heeft, dan krijgen lampje 3 en 5 beide 4V en is er nog maar (10-4-4=) 2V over, die gaat naar L1 en L2+L4 waarbij L1 het gehele overgebleven voltage krijgt en L2 en L4 deze nog moeten verdelen. Dat verklaart dat lampje 3 en 5 fel zijn, lampje 1 zachtjes brandt en lampje 2 en 4 niet zichtbaar branden, maar wel branden.



34 Fietswielen

De bezemsteel ligt los bovenop de wielen.


Als je beide wielen linksom draait, zal de bezemsteel naar links bewegen en er af vallen.
Draai je ze rechtsom, dan valt de bezemsteel er daar af.
Maar wat gebeurt er met de bezemsteel als je de wielen tegen elkaar in draait?

Maak een keuze uit onderstaande mogelijkheden:
1. De bezem blijft liggen.
2. De bezem gaat een trilling uitvoeren.
3. De bezem zal er soms links en soms rechts afvallen.
Oplossing
De prijs voor het beste antwoord gaat naar Mark Visser uit A5A van het Don Bosco College in Volendam.
Ons antwoord is: B, de bezemsteel gaat een trilling uitvoeren, want er werkt voortdurend een resulterende kracht naar het midden. Dit komt door de wrijving tussen de steel en de wielen. Daar waar de steel het meest uitsteekt, is de wrijving op de steel het grootst. Bekijk ook dit filmpje.

We komen er in Proefprikkels 10 nog op terug.



33 Natuurkundige wetten

Hieronder staan de afbeeldingen A t/m H.
Geef bij elke letter aan welke natuurkundige wet er bij hoort.

Maak een keuze uit de volgende wetten:
1. Wet van Snellius
2. Gravitatiewet
3. Wet van behoud van energie
4. Wet van Hooke
5. Wet van Ohm
6. Wet van Lenz
7. Derde wet van Newton
8. Momentenwet

A	B
C	D
E	F
G	H

Oplossing
Er kwamen geen goede oplossingen binnen.

Dit zijn de goede keuzes:
1. 3
2. 2
3. 5
4. 8
5. 6
6. 1
7. 7
8. 4






32 Fakir en haai

De haai zwemt bedachtzaam door de lucht richting de fakir. De haai is gevuld met helium. Maar hoe zit dat bij de fakir?

• Los dit raadsel op met een (bouw)tekening.


Oplossing
Er kwamen verschillende goede antwoorden binnen, maar prijs gaat naar Casper de With uit vwo 5 van het Christelijk Lyceum Veenendaal. Aan de hand van een mooie, duidelijke tekening liet hij een mogelijk ontwerp zien en benoemde hij de plek van het zwaartepunt. Hij schreef ons:

Het zit zo: onder het tapijt zit een ondersteuning of een metalen plaat of iets anders stevigs. De metalen draden gaan door de staf en de mouw van de fakir en dat wordt het zitvlak voor de fakir. Het ondersteuningsgebied is groot, zodat het zwaartepunt van de fakir daarboven zit, het is een stabiel systeem en de fakir valt niet makkelijk om.







31 Voorsprong

Kogel A wordt bovenaan een gladde cirkelvormige helling losgelaten. Op het zelfde moment wordt een identieke kogel B op de halve hoogte losgelaten.



Wat is waar?
1. Kogel B komt in een kwart van de tijd beneden.
2. Kogel B komt in de helft van de tijd beneden.
3. Beide kogels komen vrijwel tegelijk beneden.
4. Geen van de drie hierboven genoemde antwoorden klopt.


Oplossing
Er kwamen geen goede antwoorden binnen.





30 Een bol verplaatsen

Je legt de bol met massa m links in het water.


1. Hoeveel massa moet je rechts toevoegen om weer evenwicht te maken?
2. En als de bol drijft zoals een ijsblokje?
Oplossing
Er kwamen veel goede antwoorden binnen, maar de beste formulering was van Otto Kaandorp uit 6b van het Gymnasium Bernrode:
1. Als aan de linkerkant de bal met massa m wordt toegevoegd, moet je aan de rechterkant 2 ballen met massa m hebben: 2m. Je hebt namelijk al gezien dat het bakje water evenveel weegt als 1 bal met massa m. Het bakje water plus een bal met massa m heeft dus een massa van 2m net als 2 ballen met massa m.
2. Als de bal drijft betekent dat niet dat de bal zijn gewicht verliest. Dat verandert dus niks aan het evenwicht.






29 Kantje boord

Een blikje kan op zijn kant staan als het min of meer gevuld is zoals je ziet. Met een dicht blikje lukt dat niet en met een leeg blikje ook niet.


1. Doe dit na en stuur ons een foto van je opstelling.
2. Hoeveel gram water moet je minimaal aan een leeg blikje toevoegen zodat het op zijn kant blijft staan?
   En maximaal?
3. Geef in jouw foto het gebied aan waar het zwaartepunt van het blikje zich moet bevinden en licht je antwoord toe.
Oplossing
De vragen a en b leverden wel een paar goede oplossingen, maar vraag c werd alleen door Sharon Smit uit A5A op het Don Bosco College in Volendam goed beantwoord. Naar haar gaat dus de prijs. Zij schreef ons:
1. Zie afbeelding 1
2. minimale m_water ~ 49,5 gram
   maximale m_water ~ 195,5 gram.
3. Zie afbeelding 2. Het gebied waar het zwaartepunt van het blikje zich bevindt moet boven het steunpunt zijn, alleen omdat je geen vaste hoeveelheid water heb, kun je niet aangeven waar het precies ligt en heb ik dus het gebied aangegeven met een oranje rondje.

   Afbeelding 1                                                          Afbeelding 2

Onze eigen oplossing van vraag c ziet er zo uit:

Bij maximale m kantelt het blikje om het linker steunpunt; het zwaartepunt ligt dan op de linker gele lijn.
Bij minimale m kantelt het om het rechter steunpunt; het zwaartepunt ligt dan op de rechter gele lijn.
Bij tussengelegen waarden van m ligt het zwaartepunt ergens in het gearceerde gebeid.





28 Een zwevend betonblok?

Thomas More droomde in 1516 al van een materiaal waarmee huizen met dunne wanden en grote ramen konden worden gebouwd. Vijfhonderd jaar later staat onze hele wereld vol met beton.
Een vliegend betonblok voelt als utopisch. Maar ... in het stedelijk museum in Amsterdam leek een groot exemplaar te zweven. Echter, na een kwartier moesten de bezoekers de zaal verlaten of gingen de gordijntjes dicht en dat is verdacht.



Bekijk ook de film van de kunstenaars.
Heb jij een verklaring?

Oplossing
Er kwamen vrij veel oplossingen binnen met vaak creatieve suggesties, zoals: het is een hologram, er is vet veel visdraad gebruikt, er zijn drones gebruikt. Ook werd gesuggereerd dat er magneten in het spel zouden zijn. Jammer genoeg verbiedt de stelling van Earnshaw dat. De goede oplossing is: het is een soort zeppelin die met helium gevuld is. We moesten loten en de winnaar werd Pepijn Stokman uit V4B van het Amadeus Lyceum in Vleuten. Hij schreef:
"Ik denk dat het niet echt een betonblok is, maar dat het een heel goede namaak is, zoals piepschuim. Van binnen is het hol met een zak erin waar helium in zit. Die gordijntjes moeten af en toe dicht zodat de kunstenaars het blok weer kunnen bijvullen met de juiste hoeveelheid helium en het kunnen herpositioneren. Conclusie is dus dat het niet echt een betonblok is, maar eerder een soort mini zeppelin."





27 Kopzorgen

Een voetbal van 437 g en straal R = 11,0 cm, deukt tijdens deze botsingen 5,5 cm in en veroorzaakt een druk p op het hoofd van de voetballers van 1,4 bar.


  


1. Toon aan dat hier voor het oppervlak A van het platte deel van de bal geldt: A = ¾πR².
2. Schat de gemiddelde kracht op de speler.
3. Schat de snelheid waarmee de bal zal terugveren.


Oplossing
Er kwamen tien min of meer goede antwoorden binnen. De druk van 1,4 bar zal de maximale geweest zijn, maar goed, dat stond er niet duidelijk bij. We moesten loten en de winnaar bleek:
Therèse Sluys, Gerrit Rietveld College, Utrecht
1. Uit de figuur blijkt:
   r² = R² - (½R)²   ==>   r² = ¾R²   ==>   A = ¾πR²
   
   
2. Voor de maximale kracht op het hoofd geldt:
   F_max = 1,4·10⁵·¾π(11·10^-2)² = 4,0·10³ N
   Het krachtverloop tijdens het terugveren is onbekend. De gemiddelde kracht schatten wij op de helft hiervan, dus:
   F_gem = 2,0·10³ N
   
   
3. De arbeid van deze gemiddelde kracht levert de kinetische energie voor de bal en daarmee is de snelheid te berekenen:
   W = 2,0·10³·5,5·10^-2 = 1,1·10² J   ==>   v = 22 m/s






26 Mattenkloppen

a.   Leg uit welke wet de chaos in dit filmpje voorspelt (klik op onderstaand plaatje om het filmpje te bekijken).



Vraag 6 a van hoofdstuk 2 (havo en vwo) luidt:
Om welke traagheid gaat het bij mattenkloppen.

Op de site wordt dit antwoord gegeven:
De traagheid van het stof. De (zware) mat krijgt snelheid, maar staat ineens stil. Het stof schiet door en de mat blijft schoon achter.

Een gebruiker van het boek vindt dit een beter antwoord:
De traagheid van het stof. De mat krijgt plotseling snelheid door de klap en het stof (dat min of meer los verdeeld zit in de mat) blijft achter en komt zo los van de mat.

Voor beide antwoorden is wat te zeggen - tenminste als je weet hoe er 'geklopt' wordt.
b   Leg dat uit.



Oplossing
Het goede antwoord kwam van Sven van Zoggel uit klas 5A, Gymnasium Bernrode
1. De eerste wet van Newton. Massa is traag
2. Je kunt op twee manieren ’kloppen’.
   De eerste is met de mat ergens tegen aan slaan, bijvoorbeeld een muur. Dit is de uitleg van de site.
   De tweede is met een mattenklopper tegen de mat slaan. Dit is het alternatief van de gebruiker van het boek.






25 Ballon

Vraag 4 van de Nationale Wetenschapsquiz 1999 luidde als volgt:
Twee identieke ballonnen zijn met een buisje aan elkaar verbonden. In het midden van dat buisje zit een kraantje. Beide ballonnen zijn opgeblazen, de ene tot een diameter van 25 cm, de andere tot een diameter van 10 cm. Wat gebeurt er als het kraantje wordt opengedraaid?

Dit waren de antwoorden waaruit de deelnemers mochten kiezen:
• Er gebeurt niets. De ballonnen blijven even groot als ze waren
• De grote ballon loopt gedeeltelijk leeg in de kleine
• De kleine ballon loopt gedeeltelijk leeg in de grote
Uit ervaring weet je dat een ballon opblazen in het begin en aan het eind - als hij bijna knalt - moeilijk is. Dat blijkt ook uit deze grafiek; de overdruk in de ballon is p - b met b de barometerstand; r is de straal van de opgeblazen ballon en R is de straal als die nog niet onder spanning staat.
Uit de grafiek blijkt ook dat de vraag uit de Wetenschapsquiz dubieus was.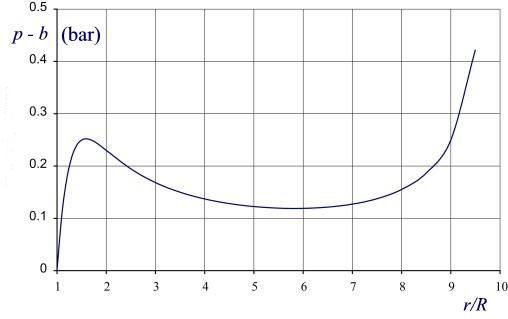




1. Wat is het goede antwoord als r_klein/R = 1,5   en   r_groot/R = 5?
2. En als r_klein/R = 4   en   r_groot/R = 9?
3. Kies vervolgens één van de volgende opdrachten:
   • Maak een film of een foto van een knallende ballon.
   • Vraag een manometer, meet de druk in een leeglopende ballon als functie van de diameter en teken de grafiek zoals hierboven voor zover mogelijk. Stuur een foto van je opstelling mee.


Oplossing
Op prijsvraag 25 kwamen geen goede antwoorden binnen. Jammer. De vragen waren dan ook pittig.
1. De kleine ballon loopt leeg in de grote. Daarbij schuift de eerste in de grafiek naar links en de tweede naar rechts.
   Die situatie kan zich voordoen als er een uitstulping ontstaat in een slagader; wordt die te groot, dan moet worden ingegrepen.
2. De grote ballon krimpt en de kleine zwelt op tot ze (na enig schommelen) even groot zijn. In de grafiek schuiven beide naar elkaar toe.
3. Dit is onze eigen meting:
   





24 De sheriff

De sheriff in een trein die met 50 m/s reed, zag een vuurgevecht op het perron tussen A en B die 50 m uit elkaar stonden. Volgens de sheriff - midden tussen A en B - schoten A en B tegelijkertijd, want hij hoorde één schot. De rechter veroordeelde echter B, omdat die volgens haar het eerste schoot.



1. Maakt het verschil of de sheriff de schoten hoorde of de flitsen zag?
2. Was de veroordeling terecht?
3. Wie werd het eerst geraakt?
4. Hoeveel tijd zat er tussen de schoten als de temperatuur 20 °C was?


Oplossing
Het beste antwoord kwam van Max Klootwijk uit V4 van het Walburg College in Zwijndrecht.
1. Ja. De snelheid van het licht (3·10⁸ m/s) is veel groter dan de snelheid van het geluid (343 m/s).
2. Nee, want de sheriff reed naar B toe en van A af. A moet dus eerder geschoten hebben.
3. B werd dus het eerst geraakt.
4. Zet de sheriff in gedachten stil. Dan krijg je
   voor A: 25 = 293t dus t = 0,0853 s
   voor B: 25 = 393t dus t = 0,0636 s
   Als de sheriff de geluiden toch tegelijk hoort, heeft A 0,022 s eerder geschoten.


23 Aan (1) of uit (0)?


a. Vul de waarheidstabel aan die bij deze schakeling hoort: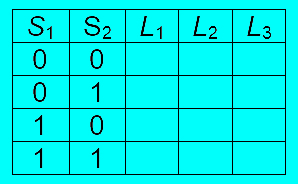

b. Welke schakeling past bij deze waarheidstabel?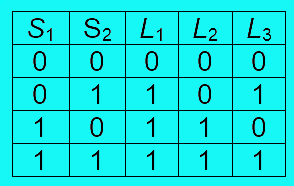



Oplossing

Er waren veel goede antwoorden zodat we moesten loten.
De gelukkige is geworden:
Lieke Stuijt uit klas A4C van het Don Bosco College in Volendam.

a.


b.




22 David en Goliath

Voordat David met een steen het voorhoofd van Goliath raakte, draaide de steen rondjes boven zijn hoofd.



1. Waarom kan dat ronddraaien niet in een horizontaal vlak plaatsvinden?
   De lengte van de leren slinger is 60 cm en de steen weegt 20 N. De maximale spankracht - zodat de slinger net niet scheurt - is 300 N.
2. Bereken het maximale toerental van de steen.




21 Rondjes draaien

Het legotandwiel met 30 tanden is vastgeplakt op tafel en kan niet draaien.
Je draait het kleine tandwiel met 20 tanden één keer om het grote tandwiel heen.



Hoeveel rondjes maakt het kleine tandwiel? Licht je antwoord toe.


De oplossing

Veel ingestuurde antwoorden gingen uit van twee tandwielen die elk om hun eigen vaste as draaien. Zij kwamen dus uit op 1,5 rondje.
Hier zit echter het grote tandwiel vast. Het kleine is een zogenaamd planetair tandwiel. Het maakt dus 2,5 rondje zoals uit deze foto's blijkt:



Marco Post uit 6a2 van het Wartburg College locatie Revius in Rotterdam heeft de prijs gewonnen. Hij schreef ons:
"Het grote tandwiel heeft 1,5 keer zoveel tanden als het kleine tandwiel. Als het kleine tandwiel een keer om het grote tandwiel heen draait passeert hij 30 tanden. Aangezien het kleine tandwiel 20 tanden heeft draait hij dan dus 1,5 rondje om zijn eigen as. Daarnaast maakt het kleine tandwiel natuurlijk ook nog een rondje om het grote tandwiel! In totaal maakt het kleine tandwiel dus 2,5 rondjes."




Voor prijsvraag 20 ontvingen we nog steeds geen inzending. Omdat we het een aardige opdracht vinden voor praktisch werk verlengen we nog één keer de inzenddatum.



20 Maak een filmpje van een waterstraal





Een soepele slang is met plakband aan een triller vastgemaakt. De straal is met een mobieltje gefilmd. Klik op de foto en bekijk ons filmpje. Verklaar de rare effecten en maak zelf zo'n filmpje.




We moesten loten bij prijsvraag 19. Bedoeld was het tunneleffect, maar wormhole, tunnelen, teleportatie e.d. beschrijven het plaatje ook.
De winnaar is geworden: Roelof Mestriner uit 5 vwo van Het Assink Lyceum in Haaksbergen.




19 Quantumwereld

Welk begrip uit de Quantumwereld wordt hier geïllustreerd?









18 De scanner in, maar welke?



a Benoem de scanners. Je mag kiezen uit: CT, MRI en PET.
A		B		C
b Kies de juiste foto’s erbij.
1		2		3
c Wat betekent dit bord?

Er waren veel goede antwoorden zodat we moesten loten.
De oplossing is:
  a.   A = MRI, B = PET, C = CT
  b.   1 (PET), 2 (MRI), 3 (CT)
  c.   Verboden voor pacemakers.

De gelukkige is geworden:
Maarten van den Berg uit klas 4 van Gymnasium Bernrode.



17 OBAFGKM

Annie Jump Canon bestudeerde honderdduizenden glasplaten met spectra van sterren.



Daardoor ontdekte ze bepaalde patronen, die ze onderbracht in eenvoudige reeksen.
Zij was de eerste die een typering invoerde op kleur in plaats van op de sterkte van de waterstoflijnen in het spectrum, wat tot dan toe gebruikelijk was.
De indeling is als volgt:

Hete, blauwe of witte sterren
     type O (blauw) - 50.000 K
     type B (blauw) - 33.000 K
     type A (wit) - 11.000 K
Gele of oranje, zonachtige sterren
     type F (wit) - 8000 K
     type G (geel) - 6000 K
     type K (oranje) - 5000 K
Koele, rode sterren
     type M (rood) - 3600 K

In de zesde editie van Binas is tabel 33 het 'Hertzsprung-Russell-diagram'.
Hierin staan sterren geclassificeerd volgens haar schema.

Waarom zij voor die letters koos, weten we niet.
Een paar oude ezelsbruggen om die letters te onthouden gaan zo:

O Be A Fine Girl Kiss Me.
Only Boys Accepting Feminism Get Kissed Meaningfully.
Oh Brother Another F's Gonna Kill Me

Wij vinden ze nogal macho, om maar te zwijgen van dit plaatje:

De prijs is gewonnen door Tamara Richardson uit vwo 6 van het Christelijk College Schaersvoorde met deze ezelsbrug:


Orion beschrijft astronomische fonkelingen gedurende koude maanden.


We hebben dit keer niet geloot. Louis schreef:
”Die van Tamara vind ik eigenlijk de beste.
Astronomisch, lyrisch en die koude maanden kloppen ook nog.”
Ruud en Hubert waren het daarmee eens.




16 Een lichtkegel

Je schijnt met een laser door een bak met kraanwater op een blanco velletje A4 en je ziet dit:



De laserstraal reflecteert diffuus tegen het vel papier. Tussen de A4 en de bak zit een heel dun laagje lucht.



De getekende gereflecteerde lichtstralen breken van lucht naar water.
1. Wat is de grootste hoek van inval i_max?
2. Bereken met i_max de bijbehorende r_max.
3. Wordt de kegel breder of smaller als je suikerwater gebruikt?
De winnaar is geworden: Bart Lammers van het Christelijk College Schaersvoorde te Aalten.

Onze oplossing is:
1. i_max = 90°.
2. r_max = g en met sing = 1/n vind je dan g = 48,6°.
3. De dichtheid van suikerwater is groter dan die van water. Daardoor neemt n toe en wordt g kleiner. De kegel wordt dus smaller.




15 Iets vergeten?

De chauffeur is met de schrik vrij gekomen en staat beteuterd naast zijn vrachtwagen.


1. Met welke wet heeft hij geen rekening gehouden?
2. Noem twee manieren hoe hij dit ongeluk had kunnen voorkomen.


Er kwamen veel antwoorden binnen uit alle delen van het land (17 verschillende scholen).
Uit de goede antwoorden moesten we loten.
De winnaar is geworden: Stijn Middelhuis van Het Assink Lyceum te Haaksbergen.

Onze oplossing is:
1. De chauffeur heeft niet aan de traagheidswet gedacht.
2. Hij had de lading beter aan de laadvloer moeten vastmaken en hij had voorzichtiger moeten remmen.
Speciale vermelding verdienen Eline en Clara van het St. Ignatiusgymnasium in Amsterdam die bedachten dat je ook kunt hopen op een noodweg!





14 De kat van Schrödinger

Op deze prijsvraag kwamen geen goede antwoorden binnen.

De oplossing:
Een toevalsschakelaar bepaalt of lampje 1 of lampje 2 aan gaat. Dan zie je óf een dode kat (1) door de halfdoorlatende spiegel S, óf een levende (2) in de weerspiegeling.



Bekijk ook de filmpjes:
• Filmpje dat eindigt met levende kat
• Filmpje dat eindigt met dode kat


In dit kistje bevindt zich de 'kat van Schrödinger'.



Of de kat dood of levend is, weet je pas als je het luikje opent.

 
Wat zit er in het kistje - behalve dan een toevalsschakelaar en twee dimlichten?




13 Nogmaals het schimmenspel
Op prijsvraag 12 kwamen geen goede antwoorden binnen. Jullie krijgen een tip en een herkansing.
Steek een stok in water en bestudeer hoe het wateroppervlak door de stok beïnvloed wordt.
Bekijk op de twee foto's nog eens hoe de stok in het water wordt gestoken.

Er kwamen geen goede inzendingen binnen.

Het antwoord:
Door de stok platter of minder plat in het water te steken kun je het wateroppervlak vervormen.


Hieronder een schaatsenrijder; zij vervormt het wateroppervlak ook. Bij felle belichting krijg je foto 2 van de prijsvraag.





Bron: TPT dec. 1998




12 Schimmenspel

Je steekt twee keer een stok in een bak water. Verklaar de verschillen in de schaduwen.










11 Een omgekeerde ’zandloper’

De vorm van een zandhoop hangt af van de vochtigheid en de grootte van de korrels. Als die glad zijn, is de hoek α klein.



Dat is ook waar voor de rode plastic bolletjes die hier in de vloeistof omhoog bewegen.



Voor de wrijvingscoefficiënt μ tussen de bolletjes onderling geldt: μ = F_w/F_n.
Bewijs: μ = tan α en bepaal de waarde van μ.

Er was één inzending die aan alle voorwaarden voldeed (bewijs en waarde van μ).
De prijs is gewonnen door Lennaert Tol uit A5A van het Don Bosco College in Volendam.

Dit is de oplossing: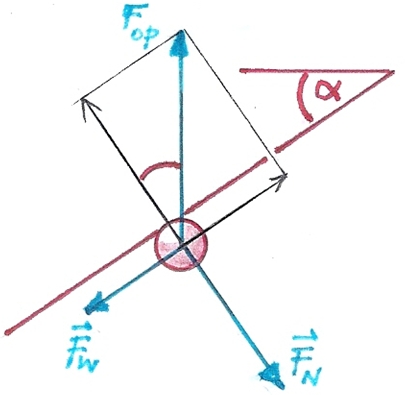


Het korreltje is in evenwicht als:
F_w = F_op·sin α
F_w = μ·F_N   met   F_N = F_op·cos α   ==>
μ·F_op·cos α = F_op·sin α   ==>   μ = tan α
We meten α = 30º   ==>   μ = 0,58




10 Bandstoot



Via de band raak je zonder effect beide andere ballen. Verwaarloos de afmetingen van de biljartballen.
Bereken hoeveel centimeter de speelbal heeft afgelegd.

Voor deze prijsvraag waren een paar goede inzendingen, zodat we moesten loten. De prijs is gewonnen door Cees Oerlemans uit 6 vwo van het Christelijk Gymnasium Utrecht.
Van Wessel Kok uit 4 havo van het Don Bosco College Volendam kregen we zo’n figuur toegestuurd:






9 Een vrieskist



Terwijl het 27 ºC is, vul je de vrieskist van 0,400 m³ voor 80% en zet je de thermostaat
op -23 ºC.
Het deksel van 1,00 bij 0,50 m krijg je de volgende dag niet meer open.
Leg met een berekening uit waarom.

De oplossing bevat deze elementen:
1. Bereken de nieuwe druk met Gay-Lussac: 8,3·10⁴ Pa
2. Bereken het drukverschil tussen binnen en buiten: 1,7·10⁴ Pa
3. Bereken de kracht op het deksel van 0,50 m²: 8,3·10³ N
4. Houd rekening met het scharnier: je hoeft maar met de helft van deze kracht te trekken, dus met 4·10³ N
5. Vergelijk deze kracht met de kracht die een mens kan leveren en concludeer dat je de kist niet open krijgt.
Er was maar één oplossingen die met al deze elementen rekening hield.
De prijs gaat naar de leerlingen uit 4a2 en 4a1 van het Warburg College, locatie Revius in Rotterdam.



8 Een viervlak

Dit viervlak bestaat uit zes weerstanden van 180 ohm. Het is aangesloten op 9,0 V.
Bereken de stroom die de bron levert en de stromen door de zes weerstanden.



De prijs gaat naar Fabian Schreurs, Rick Teuthof en Axel Valent uit A3B van het Zaanlands Lyceum. Zij hadden door dat de stroom die rechtstreeks tussen de krokodillenbekken oversteekt 50 mA is; dat de stromen via de andere hoekpunten elk 25 mA zijn en dat in de ribbe middenvoor, dankzij gelijkwaardigheid van de twee hoekpunten, geen stroom loopt. Al met al loopt er dus 100 mA.

Toa Kees Laan van het Don Bosco College in Volendam heeft dit viervlak met ledjes in elkaar gesoldeerd om te laten zien dat door één ribbe geen stroom loopt:





7 Trage gloeilampen

In de film wordt vier keer een identieke, extra gloeilamp van 100 W in serie bijgeschakeld.



De vijfde gloeilamp is het traagst van allemaal.
Dit komt natuurlijk doordat de stroom daar later aankomt.
Of niet? Stuur jouw verklaring vóór 18 januari 24:00 uur naar stevin@stevin.info en win €25.

Er kwamen geen goede oplossingen binnen. Wel hebben sommigen een klokje horen luiden, maar de klepel wist niemand te vinden.
Aan een goede oplossing stellen we deze eisen:
1. Zodra de zwarte draad ergens is ingeplugd, loopt er door alle aangesloten lampen dezelfde stroom (serie).
2. De laatst aangesloten lamp is koud en heeft een kleine weerstand (PTC).
   Volgens P = I²R wordt in die lamp minder vermogen opgewekt dan in de andere.
3. Na korte tijd hebben alle lampen dezelfde temperatuur en dus ook dezelfde R. Ze geven dan evenveel licht want de lampen zijn identiek.
4. Tijdens het opgloeien van de laatste lamp gaan de andere minder licht geven, want de totale weerstand van de kring neemt toe.




6 Drebbel?

Een verre nazaat van Cornelis Drebbel had een origineel idee: een duikboot laten opstijgen door magneten te gebruiken.



Wordt dat idee in de film gebruikt, of is er een andere verklaring voor wat je hier ziet?
Stuur je antwoord vóór 13 december 24:00 uur stevin@stevin.info en win €25.

Er kwamen geen goede oplossingen binnen. Onze oplossing is: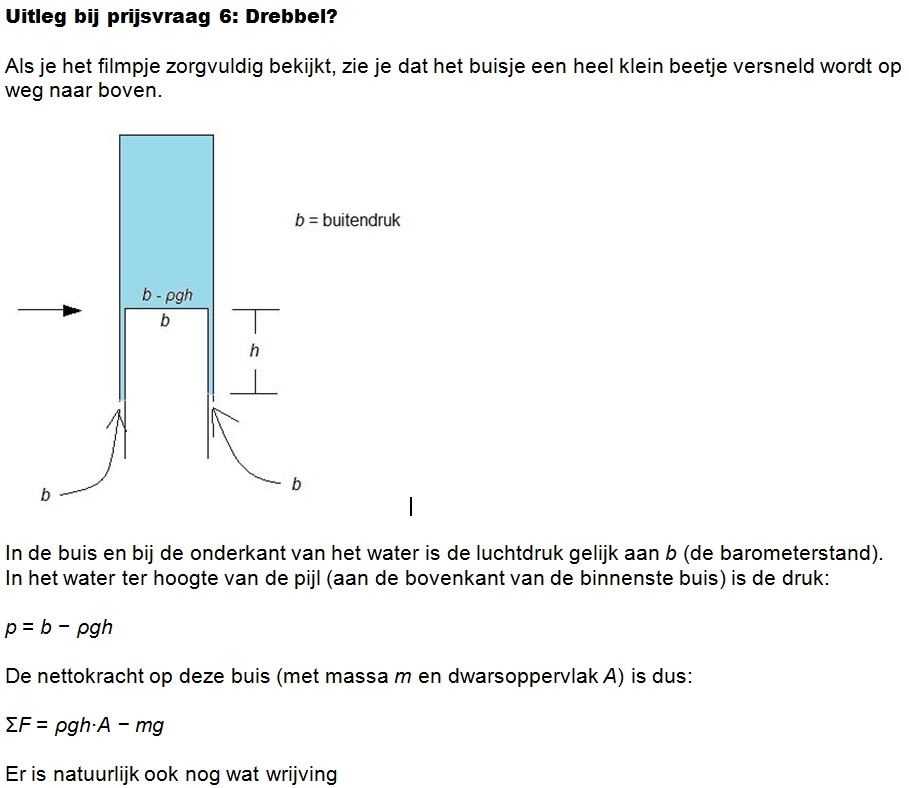





5 Treinspotten

Langs de rails staan drie waarnemers W1, W2 en W3, klaar om de lengte van een passerende trein te meten. W1 start met haar afstandsbediening de klok van W3 zo gauw de kop van de trein haar passeert. W3 stopt zijn klok als de staart hem passeert. W2 meet de passeertijd van de trein: 7,0 s.



Hoe hard reed de trein?

Voor prijsvraag 5 waren er tien goede inzendingen, zodat we moesten loten. De prijs is gewonnen door Esmée Theewis van het Geert Groote College in Amsterdam. We laten haar zelf aan het woord:

Ik denk dat het antwoord is: 20 m/s (72 km/h)
De passeertijd is 7,0 s. Dit is dus ook de tijd die de trein er over deed om vanaf de kop bij W3 tot de staart bij W3 te komen.
Dat betekent dat de trein er 18,0 - 7,0 = 11,0 s over deed om de afstand tussen W1 en W3, 220 m af te leggen.
v = x:t = 220:11=20 m/s


4 Een noodstop

De weg is weg. Je remt uit alle macht en komt net op tijd tot stilstand.
Stuurlui aan de kant beweren: je had beter een scherpe bocht kunnen maken.
Is dat zo? Leg uit.



Er kwamen geen oplossingen binnen. Onze oplossing ziet er zo uit:





3 Een dobbelsteen

De stippen lijken in de spiegel van kleur te zijn veranderd. Verklaar dit gezichtsbedrog.



Prijsvraag 3 is gewonnen door Gijs van der Gracht uit klas 5 van Gymnasium Bernrode in Heeswijk-Dinther. We laten hem zelf aan het woord:

”Ik vermoed het antwoord te weten. Volgens mij zit het zo:

De kleuren zitten in de gaten in de zijkanten van de dobbelsteen.
Nu denk ik dat de gaten maar ongeveer voor de helft zijn geverfd met kleur (zowel zwarte als rode ogen/gaten).



Dus als je er van bovenaf op kijkt, zie je alleen de onderste helft van de gaten en niet de bovenste helft.
Kijk je in de spiegel, kijk in feite van onderaf tegen de dobbelsteen op en zie je dus alleen de bovenste helft van de gaten en niet de onderste helft.
Verder:
De kleuren in de spiegel lijken nog wel enigszins op de kleuren die je ziet als je er rechtop (van bovenaf) kijkt.
Dit komt slechts door de reflectie van de kleuren die in de bovenste helft zijn geverfd.”



2 Een mini-segway of: een dubbeltje op zijn kant

Bekijk het filmpje. Leg uit hoe dit motortje werkt.
(Tip: de stuivers zitten niet met lijm aan de as vast.)



Prijsvraag 2 was moeilijk. Het beste antwoord kwam van Femke Rijfkogel van de OSG West Friesland in Hoorn. Gefeliciteerd!
We laten haar zelf aan het woord:
”Ik denk dat ik het antwoord op de prijsvraag weet.
In de cilinder zitten twee magneten die met de noordpool naar elkaar gericht zijn. Deze twee magneten willen elkaar afstoten en hierdoor ontstaan er magnetische veldlijnen die naar buiten prikken. Door de rails loopt een stroom waardoor er een lorentzkracht wordt opgewekt. Deze lorentzkracht is in deze situatie naar links gericht waardoor de cilinder gaat rollen.”


Deze foto toont hoe de dame meegesleept wordt door de as.
De bronskleurige euromunten zijn magnetiseerbaar. Zie ook Smaakmaker 4.






1 Met Stevin voor de spiegel

De opdracht was: wie kan het beste uitleggen hoe deze foto gemaakt is?


De prijsvraag is ex equo gewonnen door Kim Hofman en Nienke Meekel, leerlingen van het Don Bosco College in Volendam.

Ons antwoord ziet er zo uit:



Louis en Hubert staan beiden voor dezelfde spiegel. Hubert staat verscholen achter Louis, maar is in de spiegel zichtbaar. Er waren meer inzenders die dit doorhadden, maar alleen de twee Volendammers zagen dat Hubert met een nepboek in zijn handen stond dat er in spiegelbeeld dus goed uitzag. Deze foto was op zijn boek geplakt:



Kim en Nienke maakten ook foto's:





Op het DonBosco College bestaat de goede gewoonte dat leerlingen een extra punt kunnen verdienen met bijzondere prestaties, zoals onder andere het oplossen van onze puzzels. We geven deze tip graag door aan de docenten die met Stevin werken.